

Tiefensuche (auch Depth-First Search, kurz DFS genannt) ist ein fundamental wichtiger Algorithmus, den jede Entwicklerin und jeder Entwickler in ihrem oder seinem Werkzeugkasten haben sollte. Nicht nur hilft er bei der Navigation von Baum- und Graphstrukturen, sondern er ist auch der Schlüssel zu vielen komplexeren Algorithmen.
Die Tiefensuche hat eine breite Palette von Anwendungen in der Informatik:
Die Tiefensuche, auch bekannt als Depth-First Search (DFS), ist ein Algorithmus, der dazu verwendet wird, Knoten in einem Graph oder Baum zu durchlaufen. Dabei "taucht" er so tief wie möglich in den Graphen ein, bevor er zurückkehrt und andere Wege erkundet. Der Prozess lässt sich in klare Schritte unterteilen:
Ein wichtiger Punkt bei der Tiefensuche ist, dass sie rekursiv ist. Das bedeutet, dass der Algorithmus sich selbst immer wieder aufruft, um tiefere Ebenen des Graphen oder Baums zu erkunden. Dieser rekursive Ansatz ermöglicht es der Tiefensuche, komplex vernetzte Strukturen systematisch und gründlich zu durchsuchen.
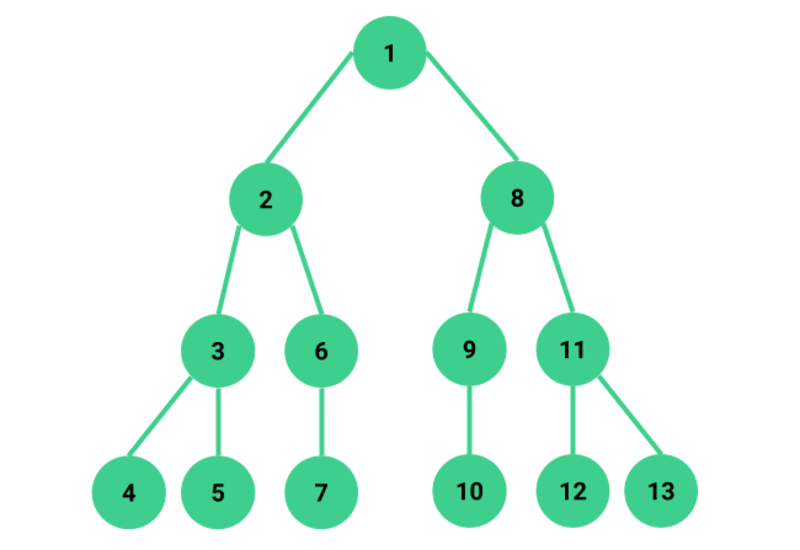
Du kannst dir die Tiefensuche wie einen Entdecker in einem Labyrinth vorstellen. Anstatt jeden möglichen Weg gleichzeitig zu erkunden, konzentriert er sich zuerst darauf, einen einzelnen Weg so weit wie möglich zu verfolgen. Erst wenn er auf eine Sackgasse stößt, kehrt er um und sucht nach anderen Wegen. So wird Schritt für Schritt das gesamte Labyrinth systematisch erkundet.
Wenn du deine Fähigkeiten im Bereich Tiefensuche testen und weiterentwickeln möchtest, bietet EntwicklerHeld einige spannende Herausforderungen. Ob es darum geht, eine Fläche in Python zu füllen, das kürzeste Wege Problem in C# zu lösen oder das klassische Türme von Hanoi Problem in JavaScript – Tiefensuche ist oft ein unverzichtbarer Bestandteil der Lösung.
Stell dir vor, du hast ein zweidimensionales Raster, und du möchtest einen bestimmten Bereich ausfüllen. Eine Möglichkeit, dies zu tun, ist die Tiefensuche. Der Grundgedanke dahinter ist simpel: Beginne an einem Punkt und "erkunde" systematisch alle benachbarten Punkte.
Pseudocode für den Flood-Fill Algorithmus mittels Tiefensuche:
FUNKTION fülleBereich(raster, x, y, alteFarbe, neueFarbe):
WENN x < 0 ODER x >= rasterBreite ODER y < 0 ODER y >= rasterHöhe:
RETURN
WENN raster[y][x] != alteFarbe:
RETURN
raster[y][x] = neueFarbe
fülleBereich(raster, x-1, y, alteFarbe, neueFarbe) // "Westen"
fülleBereich(raster, x+1, y, alteFarbe, neueFarbe) // "Osten"
fülleBereich(raster, x, y-1, alteFarbe, neueFarbe) // "Norden"
fülleBereich(raster, x, y+1, alteFarbe, neueFarbe) // "Süden"
END
In dieser Funktion wird jeder Punkt im Raster, der die alte Farbe hat, mit der neuen Farbe "übermalt". Dabei wird rekursiv in alle Richtungen weitergeforscht, bis kein benachbarter Punkt mit der alten Farbe mehr gefunden wird.
Möchtest du diesen Algorithmus in Aktion sehen? Dann versuche dich an der Python Challenge auf EntwicklerHeld, wo genau dieser Ansatz hilfreich sein kann.
Und wenn du das gemeistert hast? Dann warten noch weitere spannende Herausforderungen, wie z.B. das kürzeste Wege Problem in C# oder das faszinierende Türme von Hanoi Problem in JavaScript, auf dich! Alle kannst du mit der Tiefensuche angehen - oder du versuchst dich in einem neuen Ansatz!
Schließe dich Tausenden von Entwicklerinnen und Entwicklern auf EntwicklerHeld an und bringe deine Programmierkenntnisse auf das nächste Level! Hoffentlich hilft dir dieser Artikel dabei, ein besseres Verständnis für Tiefensuche zu bekommen und dich zu motivieren, die spannenden Herausforderungen auf EntwicklerHeld anzugehen. Viel Erfolg!